Kaggle Digit Recognizer series
Data for the digit recognizer is provided by Kaggle in csv formatted files. There are 42,000 training samples and 28,000 test samples. These can be read in to Octave with the csvread() function however this is painfully slow to witness. Much better to read the csv’s once and save the data in a more easily digestible binary format to speed up development and testing. I find it useful to have smaller slices of the data files available too. No need to throw 42,000 samples at the code when you’re just testing paths and logic. The code below reads the csv’s and saves full sized mat files along with 10%, 1%, and 0.1% slices.
%% training data set contains 42000 samples
%% the first row contains column labels
fname = 'train';
samples = csvread(strcat(fname, '.csv'));
samples = samples(2:end, :); % remove the first row (contains column labels)
rand('seed', 3.14159); % ensure this is repeatable
samples = samples(randperm(size(samples, 1)), :); % shuffle the sample order
X = samples(:, 2:end); % seperate inputs and outputs
y = samples(:, 1);
y(y==0) = 10; % change zero labels to tens to work with existing code
% save the full training data set
save('-float-binary', strcat(fname, '.mat'), 'X', 'y');
% save the abbreviated training data sets
sizes = [4200 420 42];
for s = sizes
X = X(1:s, :);
y = y(1:s, :);
save('-float-binary', strcat(fname, int2str(s), '.mat'), 'X', 'y');
end
%% test data set contains 28000 samples
%% the first row contains column labels
fname = 'test';
Xtest = csvread(strcat(fname, '.csv'));
Xtest = Xtest(2:end, :); % remove the first row (contains column labels)
% save the full test data set
save('-float-binary', strcat(fname, '.mat'), 'Xtest');
% save the abbreviated test data sets
sizes = [2800 280 28];
for s = sizes
Xtest = Xtest(1:s, :);
save('-float-binary', strcat(fname, int2str(s), '.mat'), 'Xtest');
end
i.e. train.csv has been transmogrified in to train.mat, train4200.mat, train420.mat, and train42.mat.
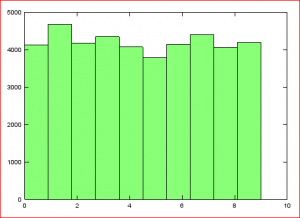
Just as a little sanity check lets have a look at how the training data target values are distributed. OK, not perfectly uniform, but a reasonable distribution of 0 through 9.
 Too cool, must learn more about this: Daniel Nouri’s Using deep learning to listen for whales uses multiple convolution layers to process inputs to a neural net. Details? Dunno much. In the whale case audio is treated as a greyscale image. Are the convolution layers treated as an independent feature generation stage in front of the neural net? Or are all weights learned together? Since convolution layer weights are shared among multiple neurons it seems a deep “normal” net could achieve similar results but may result in training times measured in archeological time units.
Too cool, must learn more about this: Daniel Nouri’s Using deep learning to listen for whales uses multiple convolution layers to process inputs to a neural net. Details? Dunno much. In the whale case audio is treated as a greyscale image. Are the convolution layers treated as an independent feature generation stage in front of the neural net? Or are all weights learned together? Since convolution layer weights are shared among multiple neurons it seems a deep “normal” net could achieve similar results but may result in training times measured in archeological time units.
 On January 21st
On January 21st