Kaggle Digit Recognizer series

From yesterday’s post:

Octave appears to be failing on the first iteration inside the fmincg() optimization function. The error message is not very helpful. It complains of being out of memory or an index exceeding its range. No line number given.

I could not reproduce this failure. This was on a “fresh” run of Octave so perhaps it was caused by some weird program state left over from ongoing development. Note to self: try restarting Octave when mysterious crashes with unhelpful error messages occur.

So then before the science begins let’s try one more Kaggle submission, this time using all 42,000 samples to train the neural network. Same as last attempt are the 350 and 100 node hidden layers, lambda 1, and 500 training iterations. Run time was about 5000 seconds (1 hour, 13 minutes), final cost function 0.0671, and self-classified accuracy 99.714%.

Slight improvement but probably not meaningful. There is so much random stuff going on here, from the random initialization of Thetas, to whatever random selection is done at Kaggle in scoring the results. The cross validation and analysis discussed at the end of yesterday’s post really are next.

Kaggle Digit Recognizer series

The initial results (previous post) for the digit classifier were coming in with an accuracy 4 points below the Kaggle-provided sample solutions. This was with only two naive attempts. First was a neural net with a 25-node hidden layer trained over 50 iterations. Next was a net with a 300-node hidden layer trained for 5000 iterations. Some improvement may be gained by tuning the regularization lambda. However no training data subsetting and cross validation has been done yet towards this goal.

It seemed reasonable (and interesting!) to modify the code to allow a second hidden node layer in pursuit of better results. Where to start? The new code will be cloned from what is already working. The single hidden layer functions will remain intact to allow easy side-by-side testing of solutions. The cost function clearly needs to change so nnCostFunction2H() will be used for that. I’m adopting a 2H suffix for functions which support the dual hidden layer network model.

I like the confidence that comes from checking the cost function’s gradients against computed numerical gradients so there will be a checkNNGradients2H() as well.

A predict2H() will be needed too. It would be preferable to have all the training and test data prediction code together in a single function. But at this point in development I would rather have the single and dual hidden layer top level orchestration code in separate files to avoid if-then toxemia in getting all the bits right. Therefore we’ll have trainNN2H.m and runNN2H.m as top level scripts for training the net and producing predicted classifications for submission to Kaggle.

So the changes are really not that extensive. They must be precise though, no room to get sloppy if the vectorized code is expected to work properly. The part of the existing code that was bothering me most deals with reconstructing the Theta matrices. I think there is too much math going on as parameters to the reshape() function calls. I find code like this hard to read and frightening to consider extending:

% Obtain Theta1 and Theta2 back from nn_params
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)), ...
                 hidden_layer_size, (input_layer_size + 1));

Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), ...
                 num_labels, (hidden_layer_size + 1));

I need a picture of what is happening here!

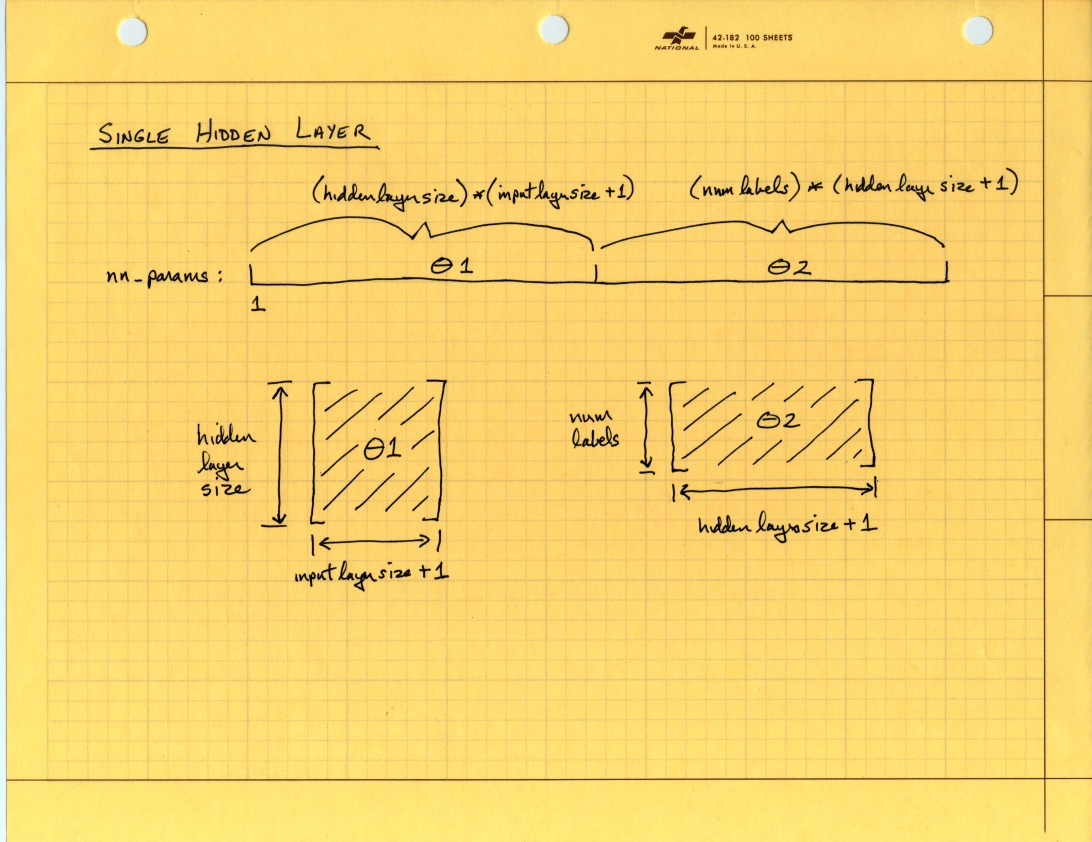
So then for two hidden layers Theta recovery will look like this:

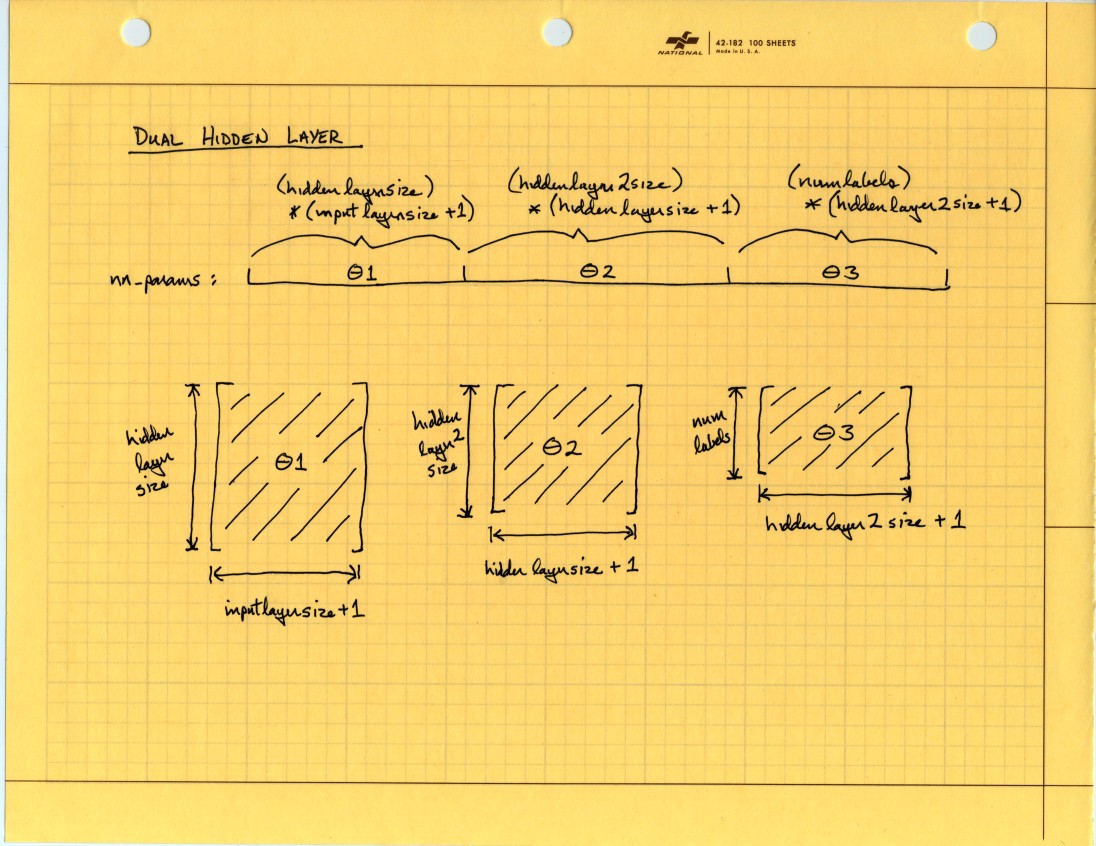
And from that picture I can see a pattern of how the Theta dimensions progress giving me a pretty good idea how to proceed if I want to parameterize the hidden layer depth. Also, the Theta recovery is done in at least two places in the existing code so I’ve replaced it with a function:

function [Theta1 Theta2 Theta3] = reshapeTheta2H(nn_params, ...
                                                 input_layer_size, ...
                                                 hidden_layer_size, ...
                                                 hidden_layer2_size, ...
                                                 num_labels)
%reshapeTheta2H Recovers Theta matrices for 2 hidden layer NN from flattened vector

    Theta1_size = hidden_layer_size * (input_layer_size + 1);
    Theta2_size = hidden_layer2_size * (hidden_layer_size + 1);
    Theta3_size = num_labels * (hidden_layer2_size + 1);

    Theta1_start = 1;
    Theta2_start = Theta1_size + 1;
    Theta3_start = Theta1_size + Theta2_size + 1;

    Theta1 = reshape(nn_params(Theta1_start : Theta1_size), ...
                     hidden_layer_size, (input_layer_size + 1));

    Theta2 = reshape(nn_params(Theta2_start : (Theta1_size + Theta2_size)), ...
                     hidden_layer2_size, (hidden_layer_size + 1));

    Theta3 = reshape(nn_params(Theta3_start : end), ...
                     num_labels, (hidden_layer2_size + 1));

end

Now another naive test run, no regularization tuning yet. This neural net will use 350 nodes in the first hidden layer, 100 nodes in the second hidden layer, lambda = 1, and 500 training iterations. The full training set of 42,000 samples will be used.

But no! Octave appears to be failing on the first iteration inside the fmincg() optimization function. The error message is not very helpful. It complains of being out of memory or an index exceeding its range. No line number given. This needs investigation but not right now, I’d really like to see some results.

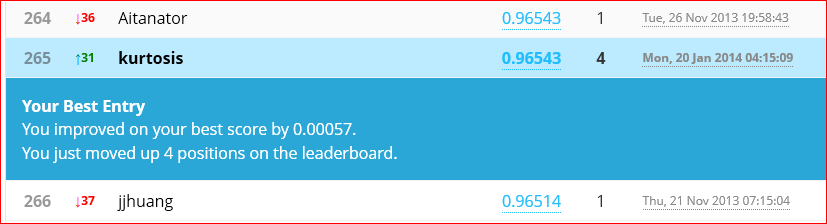
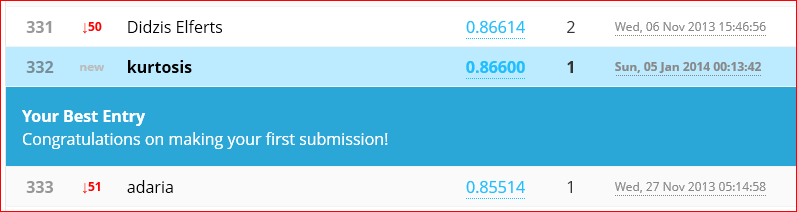
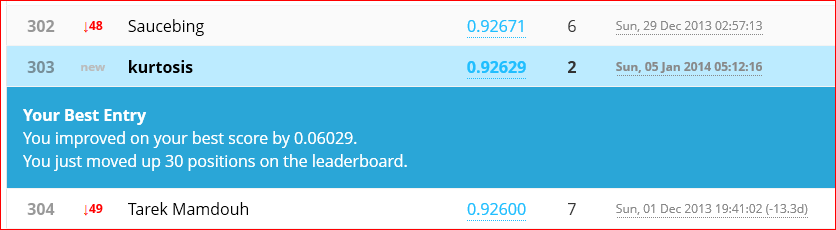
Cutting down the training set size by 20% to 33,600 samples works with no complaints. Run time is just under 3600 seconds (1 hour). Final iteration (500) cost function value is 0.0596 and self-classified accuracy is 99.821%. The Kaggle submission for this net scored 96.486% accuracy.

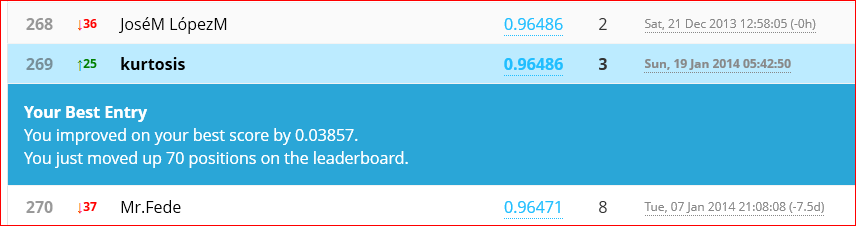
That is an improvement, but not so much. It is still under the Kaggle sample solution performance but getting closer. Now it’s time to put the science in Data Science. Next to-do is cross validation to find a proper lambda. And next after that will be examining training vs cross validation error rates over a range of sample set sizes. This should tell if the model is having trouble with high bias or high variance.

Kaggle Digit Recognizer series

For this first attempt at getting actual Kaggle classification results the neural network from the Machine Learning course will only be changed in its input size dimension. A single hidden layer with 25 units is used. The default of 50 iterations for training and lambda of 1 for regularization will be used.

A little code rearrangement is in order here too. Some things in ex4.m aren’t needed (parts 2 through 5). Most of its remaining logic gets moved in to trainNN.m and a few lines are added to save the trained Theta matrices. New is runNN.m which loads Thetas, runs sample data through the network, and saves results in a Kaggle submission friendly format like so:

%% runNN.m

thetaFile = 'Thetas.mat';
testDataFile = 'test.mat';
resultsFile = 'results.csv';

% load trained model theta matrices
load(thetaFile);

% load test data
load(testDataFile);

% predict outputs from test samples
pred = predict(Theta1, Theta2, Xtest);

% change 10 labels back to 0 for Kaggle results
pred(pred==10) = 0;

% save predicted results
outfd = fopen(resultsFile, 'w');
fprintf(outfd, 'ImageId,Label\n');
for n = 1:size(pred)
	fprintf(outfd, '%d,%d\n', n, pred(n));
end
fclose(outfd);

Initial training of the net was done with all 42,000 samples. Splitting the data in to training and validation sets will be done later. After 50 training iterations the cost function value was 1.19. The network self-classified its training data with 87.698% accuracy. The initial Kaggle submission of the test data set achieved 86.600% accuracy, well behind the two Kaggle sample solutions with lots of room for improvement.

For an unguided attempt at improving on this result I trained a new network with 300 hidden nodes (still single layer) over 5000 iterations. Final self-classified accuracy was 100% and cost function was 0.0192. Run time for this was about 4200 seconds vs 10 seconds for the previous attempt. The Kaggle submission from this net was 92.629% accurate.

Kaggle Digit Recognizer series

Sample data from the Machine Learning class is arranged as one sample per row with data values ranging from just a bit below 0 to a little above 1. Each digit image is a flattened 20×20 grey scale pixel array. The Kaggle data is arranged similarly but values range from 0 to 255. Kaggle digits are flattened 28×28 pixel arrays. The difference in value ranges should not be a problem for the exisiting code. The neural network input layer for Kaggle data will have 784 units vs the 400 used for the ML class data.

So the only code modification at this point is changing:

input_layer_size  = 400;  % 20x20 Input Images of Digits
hidden_layer_size = 25;   % 25 hidden units
num_labels = 10;          % 10 labels, from 1 to 10

to this:

input_layer_size  = 784;  % 28x28 Input Images of Digits
hidden_layer_size = 25;   % 25 hidden units
num_labels = 10;          % 10 labels, from 1 to 10

So we should be ready to go! The first thing we see running the top level Octave code is an image of a random selection of input samples.

What? This can’t be right! Well it doesn’t really matter to the performance of classifying digit samples. But it is rather awkward to turn your head 90 degrees and look in a mirror at the computer display so lets fix this. The problem is caused by a difference of opinion on up/down/left/right for the two data sources. To fix this the displayData() function needs a change where the display_array is being accumulated. Change this:

        reshape(X(curr_ex, :), example_height, example_width) / max_val;

to this:

        reshape(X(curr_ex, :), example_height, example_width)' / max_val;

That’s it. Just transpose the result of reshape. A single character change.

Much better.

Kaggle Digit Recognizer series

Data for the digit recognizer is provided by Kaggle in csv formatted files. There are 42,000 training samples and 28,000 test samples. These can be read in to Octave with the csvread() function however this is painfully slow to witness. Much better to read the csv’s once and save the data in a more easily digestible binary format to speed up development and testing. I find it useful to have smaller slices of the data files available too. No need to throw 42,000 samples at the code when you’re just testing paths and logic. The code below reads the csv’s and saves full sized mat files along with 10%, 1%, and 0.1% slices.

%% training data set contains 42000 samples
%% the first row contains column labels

fname = 'train';
samples = csvread(strcat(fname, '.csv'));

samples = samples(2:end, :); % remove the first row (contains column labels)

rand('seed', 3.14159); % ensure this is repeatable
samples = samples(randperm(size(samples, 1)), :); % shuffle the sample order

X = samples(:, 2:end); % seperate inputs and outputs
y = samples(:, 1);

y(y==0) = 10; % change zero labels to tens to work with existing code

% save the full training data set
save('-float-binary', strcat(fname, '.mat'), 'X', 'y');

% save the abbreviated training data sets
sizes = [4200 420 42];
for s = sizes
    X = X(1:s, :);
    y = y(1:s, :);
    save('-float-binary', strcat(fname, int2str(s), '.mat'), 'X', 'y');
end

%% test data set contains 28000 samples
%% the first row contains column labels

fname = 'test';

Xtest = csvread(strcat(fname, '.csv'));

Xtest = Xtest(2:end, :); % remove the first row (contains column labels)

% save the full test data set
save('-float-binary', strcat(fname, '.mat'), 'Xtest');

% save the abbreviated test data sets
sizes = [2800 280 28];
for s = sizes
    Xtest = Xtest(1:s, :);
    save('-float-binary', strcat(fname, int2str(s), '.mat'), 'Xtest');
end

i.e. train.csv has been transmogrified in to train.mat, train4200.mat, train420.mat, and train42.mat.

Just as a little sanity check lets have a look at how the training data target values are distributed. OK, not perfectly uniform, but a reasonable distribution of 0 through 9.

Kaggle Digit Recognizer series

What is a good performance goal? If this problem were being started from scratch it would be reasonable to create a baseline classifier by a simple method such as counting each digit’s population in the training set and selecting the most abundant member as the  answer in all cases. In an evenly distributed population this would give an answer that was correct 10% of the time. It shouldn’t be too hard to beat that with a moderately more sophisticated classifier.

It’s not going to be that easy with this problem though. Kaggle has provided two sample solutions. First is a random forest which uses 1000 decision trees and votes on the digit identification. The other is a nearest-neighbor classifier that finds the 10 euclidean-closest trained samples and votes on its solution. These set the bar pretty high. The competition’s leader board shows them scoring 96.829% and 96.557% on test data submissions.

Kaggle Digit Recognizer series

So you’ve completed Andrew Ng’s course on Machine Learning offered through Coursera. Now can the Octave code used for the neural network assignment be adapted for the Kagle Digit Recognizer competition and produce a reasonable performing entry?

Posts in this series will all be tagged with Kaggle-Digits.